ESTIMADOR:
En estadistica, un estimador es un estadistico (esto es, una función de la muestra) usado para estimar un parámetro desconocido de la población. Por ejemplo, si se desea conocer el precio medio de un artículo (el parámetro desconocido) se recogerán observaciones del precio de dicho artículo en diversos establecimientos (la muestra) y la media aritmética de las observaciones puede utilizarse como estimador del precio medio.
Para cada parámetro pueden existir varios estimadores diferentes. En general, escogeremos el estimador que posea mejores propiedades que los restantes, como insesgadez, eficiencia, convergencia y robustez (consistencia).
El valor de un estimador proporciona lo que se denomina en estadística una estimación puntual del valor del parámetro en estudio. En general, se suele preferir realizar una estimación mediante un intervalo, esto es, obtener un intervalo [a,b] dentro del cual se espera esté el valor real del parámetro con un cierto nivel de confianza. Utilizar un intervalo resulta más informativo, al proporcionar información sobre el posible error de estimación, asociado con la amplitud de dicho intervalo. El nivel de confianza es la probabilidad de que a priori el verdadero valor del parámetro quede contenido en el intervalo.
En la práctica, en los intervalos suelen indicarse dando el valor del estimador puntual utilizado como centro del intervalo y un valor que debe sumarse y restarse para obtener el límite superior e inferior, por ejemplo:
equivale a ![[3,5-2,03\,;\,3,5+2,03]=[1,47\,;\,5,53]](http://upload.wikimedia.org/math/3/a/2/3a27850f0e5e6e074976ff0802e006d1.png)
y 
son ambos estimadores de θ y
diremos que es más eficiente que . Un estimador es más eficiente (más preciso), por tanto, cuanto menor es su varianza.
es más eficiente que . Un estimador es más eficiente (más preciso), por tanto, cuanto menor es su varianza.La eficiencia de los estimadores está limitada por las características de la distribución de probabilidad de la muestra de la que proceden. El teorema de Cramer-Rao determina que la varianza de un estimador insesgado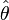 
de un parámetro θ es, como mínimo,
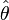de un parámetro θ es, como mínimo,![\mathrm{var} \left(\widehat{\theta}\right)
\geq
\frac{1}
{
\mathrm{E}
\left[
\left[
\frac{\partial}{\partial \theta} \log f(X;\theta)
\right]^2
\right]
}](http://upload.wikimedia.org/math/a/c/c/acc2d5de7ab27f4493fa9477eab6c335.png)
donde f(X;θ) es la funciones de densidad de probabilidad de la muestra 
en función del parámetro θ, (denominada funciones de verosimilitud). Si un estimador alcanza esta cota mínima, entonces se dice que el estimador es de mínima varianza.
en función del parámetro θ, (denominada funciones de verosimilitud). Si un estimador alcanza esta cota mínima, entonces se dice que el estimador es de mínima varianza.
